√70以上 球 体積 求め方 積分 115223-球 体積 求め方 積分

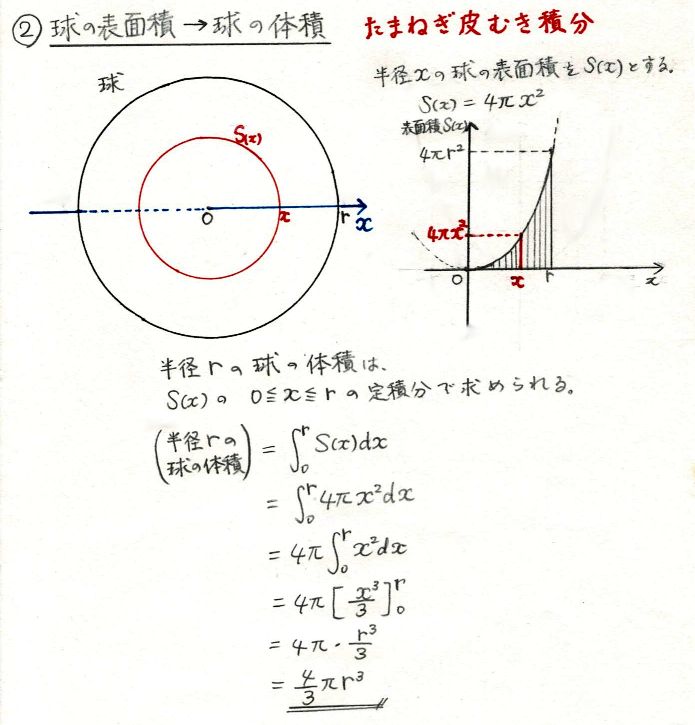
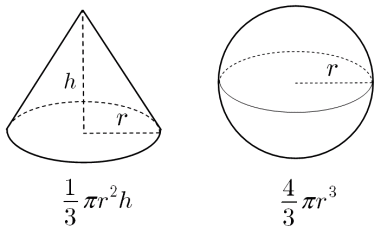
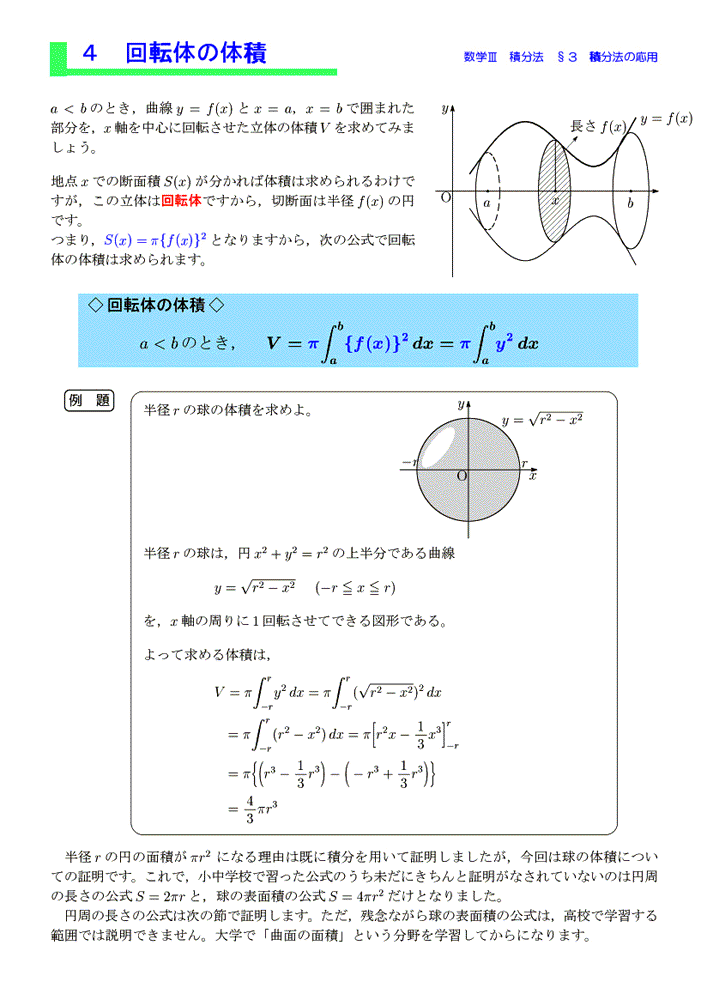
定積分の応用 §3 積分法 7定積分 (回転体の体積) 小学校や中学校で， 三角すいの体積 三角すいの体積： 球の体積： であることは，学習したと思います。 その時，「どうして円すいの体積が，円柱の体積の3分の1になっているのか？ 体積・表面積の公式や求め方、証明（積分）と計算問題 この記事では、「球」の公式（体積・表面積）や求め方をできるだけわかりやすく解説していきます。 また、なぜ公式が成り立つかも証明していきます。 この記事を通してぜひマスターして①球の体積の公式の求め方 球の表面積の公式の求め方について考察する前段階として、球の体積の公式の求め方を 考察しておこう。下の図1において、球の中心から距離 x の点で切った断面である円の半径は √(r 2 －x 2) であるから、円の面積は、S(x)＝π(r

4次元物体の表面積はどうやって計算するのですか Quora

球 体積 求め方 積分

球 体積 求め方 積分-球の体積を求める公式は、V = 4/3 πr^3 で表されます。このページでは、例題と共に、この公式の使い方を説明しています。 下記の記事で、\(n\)次元空間の半径\(R\)の球の体積というのを求めました。 前回の記事はこちら n次元空間における半径Rの球の体積 ↑結果はこちらです。 せっかくなので、2次元、3次元、4次元、5次元の球の体積

例題対比 球の体積と表面積

重心と積分の考え方 工学院大学の学生のみ利用可：印刷不可：再配布不可 (c)加藤潔18 1 半径rの一様な球の体積 なので，その位置を求める うさぎでもわかる解析 Part27 2重積分の応用（体積・曲面積の求め方） 19年11月4日 21年7月16日 49分1秒 ももうさ スポンサードリンク こんにちは、ももやまです。 今回は2重積分を使って立体の体積や曲面積（表面積）を求める方法についてまとめてい(2)円の面積、(4)球の体積について、 温故知新ラーニングのイメージ表現をしていきます。 (2)円の面積 (4)球の体積 2通りのイメージで求めてみます！ 注）「偶関数」とは、縦のS(x)軸に関して対称の関

 球の体積の求め方の公式が覚えられねえ！！ こんにちは！この記事をかいているKenだよ。ビニール傘を買っちゃったね。 球の体積の求め方には公式があるんだ。 球の半径をrとすると、体積の求め方は、 $$\frac{4}{3}πr^3$$ になるよ。 つまり、（体積の計算） 立体の体積を求めるには，体積の微分が断面積になることを利用します． すなわち，左端 a から座標 x までの区間にある体積を x の関数として V(x) で表し， x における断面積を S(x) とおきます． 上で復習した面積の求め方と同様にして体積V＝（4π／3） r 3 になることがわかりました。 この様に、要素に分割して総和を計算することが「積分」をするということです。 別解 以下の様に、直接に球の体積を求めることもできます。 先ず、半径1の球の体積を計算します。

球座標の座標曲線に沿う線積分の求め方について説明しよう そのために, 例としてr 曲 線に沿う線積分を考える ベクトル場V は球座標の成分をもちいて V = Vr(r,θ,φ)er Vθ(r,θ,φ)eθ Vφ(r,θ,φ)eφ (11) と表されるとする また, 積分経路として球の体積 110 /80件 表示件数 5 10 30 50 100 0 1 1607 歳未満 / 小・中学生 / 非常に役に立った / 使用目的 関数グラフでオリンピックのロゴを作るときの計算に役立った 2 1306 歳代 / 高校・専門・大学生・大学院生 / 役に立った / 使用 球欠，球台の体積と球冠，球帯の表面積 レベル ★ マニアック 積分 更新日時 球を平面で切り取った立体の体積，および側面の面積の求め方を解説します。 結果を覚える必要はありませんが，導出方法はマスターしておきましょう。 目次 球を

球の体積 表面積 中学生にも納得のいく方法で 積分でも出します Youtube

勉強しよう数学 球の表面積を積分で求める

ことは普通困難である。大日本図書『数学の世界1』の 考え方と同様な方法で、球の体積から表面積を求め ておいた。 大学の数学、とりわけ微分積分の初期に習う重積分を使って球の表面積と体積の公式を導くことができる。 このブログでは、古典的 な 球冠，球帯の面積の求め方 Osaka University 球冠，球帯の面積の求め方 球をある平面で切り取った部分， 球冠 ，の表面積は，以下の図で示すように， 積分範囲を，0からl 2 までにすればよいので， と表すことができます． となり、 球の表面積と体積は（積分を使って計算していくと4倍になることがわかります。時間がある方は計算してみてください。） よって、半径をrとすると、球の表面積の式は、 になります。 3．球の体積を求める方法 球

球の表面積と体積の公式 数学fun

答641 球冠の体積 解答集

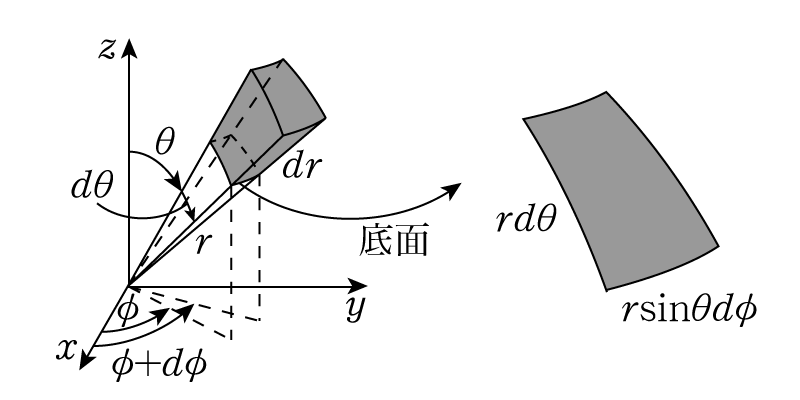
体積を求める時に積分を使うと簡単です。 最初にの微分がになる意味を考えます。 そして、面積の積分の意味を考え、球の体積やの積分をします。 ここから回転体の体積を簡単に求めることもできます。 さらに、応用もやってみましょう。 3次元球の体積 3次元球 の体積を求めます。 「 極座標のヤコビ行列とヤコビアン ： 3次元 」より、3次元 極座標 の体積要素は となるので（ 積分 範囲も注意） まさしく「球の体積の公式」。 解析入門 Ⅰ (基礎数学2) 作者 杉浦 光夫 東京大学出版会 Amazon例 3 63 (球の体積) 半径 の球の体積は である． これを多重積分で求める． （その 1） 球を 8 等分し底面が

例題対比 球の体積と表面積

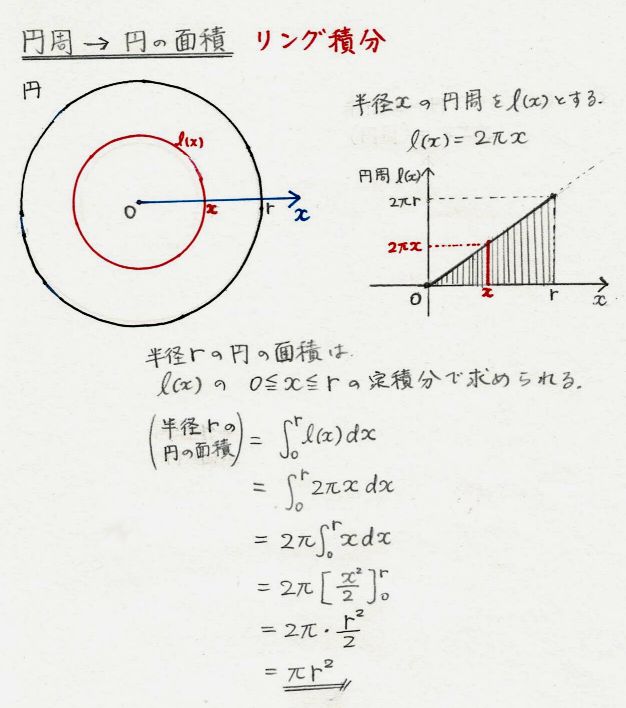
円の面積 球の体積公式の証明 理系ノート

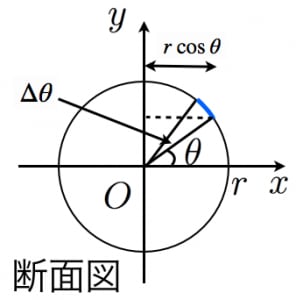
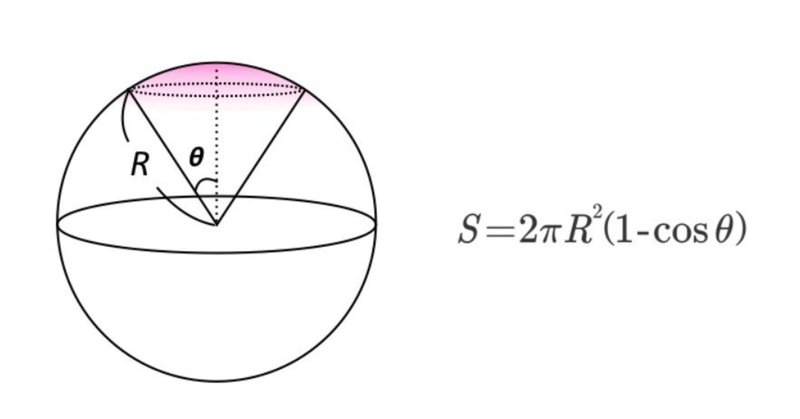
3、球の体積の求め方 円の面積の初等的な求め方は簡単だ。 でも、そこには積分の初期的な概念がある。 では、その初歩的な概念から積分へはどうやって至るのだろうか。 その積分を身体で感じるために、簡単に求まる円の面積を積分で求めてみよう。 数学 微分積分 球の半径が毎秒2cm増加して半径が10cmになった。 このときの球の体積及び表面積の変化率を求めよ 答え 体積の変化率 800π(cm^3/s) 面積の変化率160π(cm^2/s) この問題の解き方を教えてください。 求め方2：球体の体積を用いる方法 求め方1：微小の範囲を考える方法 考え方 青い部分の面積 を考える． 幅は 、長さは なので， より微小な角度を考える 球全体で積分する 計算 求め方2：球の体積を用いる方法 考え方 半径 の球の表面積を とおく

球 の 体 積 編 集 2 つ の 立 体 の 切り口 青 い 部 分 は 面 積 が 等しい

Mathematics 球の体積と表面積を求める公式 働きアリ

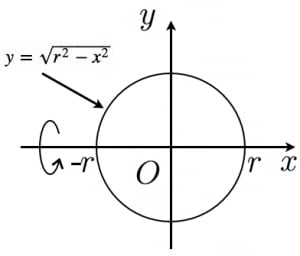
体積を数値積分で求めることを考えてみましょう。ここでは球の体積を求めること を考えます。 まず、 高校の数学3の復習です。平面に半径1の円を描き、 それをx軸もしくはy 軸について回転させれば、半径1の球が出来上がります。したがって、この性質を 数学 球の体積を求める時の積分範囲が r方向が0からr θ方向が0からπ φ方向が0から2π になる理由が分かりません。 なぜθ方向も球なんだから2πまで積分しないのかわかりません。 それ このことから、球の体積か球の表面積のいずれかを知っていればもう片方は計算できることになります。 例えば球の体積の公式を忘れてしまった！という場合は、表面積\( \displaystyle 4\pi r^2 \)を積分して\( \displaystyle \frac{4}{3}\pi r^3\)と導くことができます。

体積を求める

研究

141注1 線積分の引き戻し公式：式() 曲線 上で与えられた線密度 を、 上で積分したもの は で与えられる。 この積分を数直線上の区間 （ ） に引き戻す公式は、以下のようになる： （ ） （あえてルート記号を残しているのは、後述の面積分()や体積積分と合わせるためである。と、その前にまず、球の体積を求める公式が $ \frac{4}{3} \pi r^3 $ であることを確認しておきましょう。 この公式は「積分」によって求まるのですが、今のところ受け入れてください。作成者 積分ではスライスした円柱を積み上げる。 円柱の体積＝半径×半径×π×dxだから簡単に求めることができる。 図は内側の体積だが、これを外側でも求めた場合にも一致する。

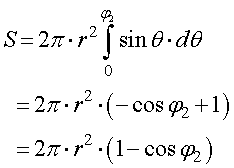
Sphere 02

数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ

解き方を確認！ 問題（ニューアクションβより） 半径1㎝の球があり、今後この球の半径は毎秒1㎝の割合で大きくなっていく。 球の表面積Sおよび体積Vの5秒後の変化率を求めよ。 まずは、SとVの式を作りましょう。 そして、それらを微分することで楕円の面積と楕円体の体積の求め方 korokoro 年10月7日 こんにちは（ @t_kun_kamakiri ）。 さてこの記事を読みに来た方は、「楕円の面積や体積の公式」を求めてきたことだと思います。 あるいは、楕円の面積や体積の公式はどうやって導かれるのかと知りLNGタンク想定して、液面高さと表面積・体積の計算に使用 アンケートにご協力頂き有り難うございました。 送信を完了しました。 一部が欠けた球の体積 のアンケート記入欄 年齢 歳未満 歳代 30歳代 40歳代 50歳代 60歳以上 職業 小・中学生 高校

球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張

体積を求める

 球の体積の公式とその覚え方・語呂合わせ 球の体積の公式 球の体積を求める公式は以下の通りです。 球の体積は半径rのとき、 \(\frac{4}{3}πr^3\) となります。 球の体積の証明のためには積分を利用する必要があり、少し難易度が高くなっています。

球の体積公式の微分が表面積になっている理由 Youtube

積分球公式球的體積 Jvvx

球の表面積と円の面積 球の表面積や円の面積を積分により求める場合 パラメ Okwave

球体の表面積 積分で求める方法 うちーノート

回転楕円体の体積 理系ノート

球の体積の求め方とその証明 高等学校で学ぶ積分の知識が必要

中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく

1

球の表面積の公式の求め方

1

球の表面積 体積 身勝手な主張

電気磁気学i Ii 要点 後藤 電気電子システム工学科 中部大学

球の体積を重積分で求めたいのですが 上手くいきません は球の上半分 半球 Yahoo 知恵袋

楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ

中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく

積分を使った球の体積の求め方です 画像のように切って切って Yahoo 知恵袋

大学入試問題

多重積分の極座標変換 物理の学校

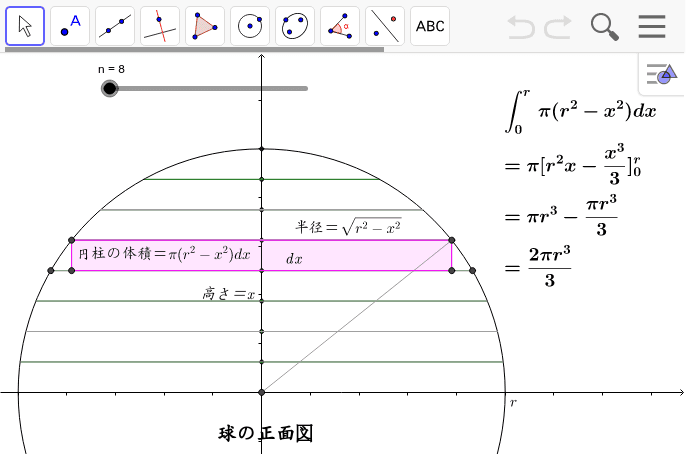
球の体積と表面積を積分で証明 高校数学の美しい物語

球の表面積の公式について みたにっき はてな

球体の体積 積分で求める方法 うちーノート

球体の表面積を 積分で求めて下さい 塾で積分を習ったのですが そのとき 球 Yahoo 知恵袋

簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく

定積分と面積3 球の表面積 Youtube

球の表面積と体積の公式 数学fun

ベクトルポテンシャル補足 １２ での 球の表面積 を求める証明 Jo3krpの独り言

球の体積 球の表面積の公式の導出 積分 優技録

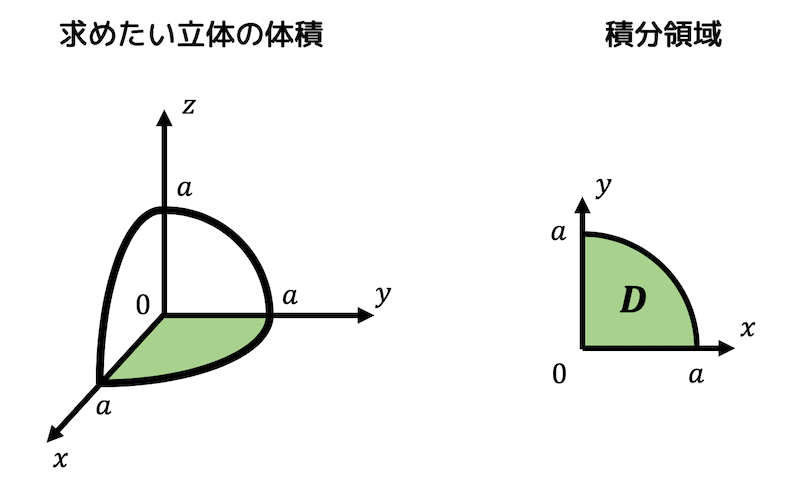
うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾

球の表面積の公式について みたにっき はてな

体積と積分 Geogebra

初等幾何 球の表面積を求める 大人が学び直す数学

球の表面積を重積分を使って計算してみた Youtube

球面積計算球 Yxhsa

高校数学 楕円の面積と回転体の体積 受験の月

球の体積と表面積を積分で証明 高校数学の美しい物語

3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ

球の体積の積分 Geogebra

球の体積 球の表面積の公式の導出 積分 優技録

４次元の球の体積 テンメイのｒｕｎ ｂｉｋｅ

Sphere 01

最も好ましい 公式 球 の 体積 ニスヌーピー 壁紙

球に関する公式 理数系無料オンライン学習 Kori

あんじょう勉強 家庭教師のつぶやき

楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ

球帯と球冠

一部が欠けた弓形の回転体の体積 高精度計算サイト

数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ

球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典

積分 体積を求める 大人が学び直す数学

勉強しよう数学 球の体積を積分で求める

球の表面積の求め方 公式と計算例

体積の求め方 回転体ではない立体を積分で 数学の偏差値を上げて合格を目指す

数学 球の表面積を積分で計算してもうまくいかない人へ

最も好ましい 公式 球 の 体積 ニスヌーピー 壁紙

数 積分 積分で球の体積を求めてみる Youtube

球の表面積の公式の求め方

数学 球の表面積を積分で計算してもうまくいかない人へ

球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張

数学講師必見 中学数学でも必須 球の体積 表面積の覚え方と導出まとめ 高校数学 塾講師ステーション情報局

数学 球の表面積を積分で計算してもうまくいかない人へ

数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ

中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく

球に関する公式 理数系無料オンライン学習 Kori

1

球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張

球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ

球の表面積の求め方 その３ 感じる科学 味わう数学

球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典

球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学

球の体積と表面積を積分で証明 京大卒が解説 高校数学 テラコヤプラス By Ameba

うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾

数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ

研究

球欠と球冠 Fukusukeの数学めも

数学 球の表面積を積分で計算してもうまくいかない人へ

4次元物体の表面積はどうやって計算するのですか Quora

球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張

球の体積の公式を積分を使わず導く 中受でも出るかも 兄中学生活

球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典

28で見込む部分の球の表面積の計算 Matsubayashi Note

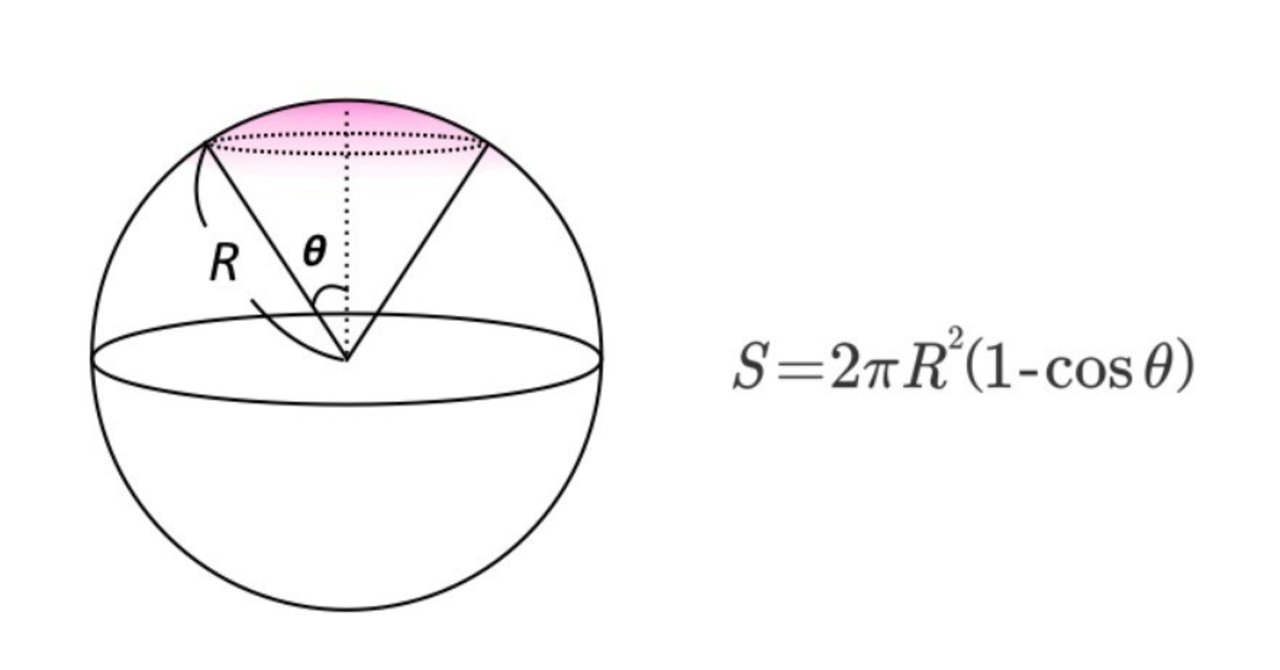
28で見込む部分の球の表面積の計算 Matsubayashi Note

高校数学 球に内接する直円錐の体積 側面積の最大値 受験の月

ｑ ｅ ｄ 証明終了 のタイトルバック２ 球の体積の重積分 テンメイのｒｕｎ ｂｉｋｅ

回転体の表面積 側面積 身勝手な主張

球の表面積の求め方 中学生の子に公式の覚え方のコツを紹介 中学や高校の数学の計算問題

数学 For 大学受験 問題 2回回転させてできる立体の体積 Mathworld4 数学iii 体積 回転体 T Co Pse9qwp78d Twitter

球の体積と表面積を積分で証明 高校数学の美しい物語

体積積分 回転体積分 京極一樹の数学塾

1

球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学

Incoming Term: 球 体積 求め方 積分,